[论文笔记]Towards Plausible Graph Anonymization图匿名化

2020 NDSS accepted paper： Towards Plausible Graph Anonymization

从社交网络导出的图数据包含了许多对工业、学术有价值的信息，同时也包含了比较敏感的隐私信息，例如一个用户的社交关系，从中可以推导出ta的不少隐私属性。因此，在公开发布这样的图数据时，需要先进行匿名化。

衡量图的匿名化程度有一些可以借鉴的度量，例如数据库的k-anonymity：一个发布的数据库中，一条个人的信息至少无法与其他k-1个人的区分开。在图数据中，(k, l)-anonymity指的是一个节点至少与k-1个其他节点拥有l个相同的邻居。也有一些算法基于度数来定义k-anonymity： 一个节点至少有k-1个其他节点和它度数相同。

当前，图匿名化的主流方法是在图的边集中加入干扰，如在图中加入一些fake的边（或者减少一些边，但是因为减少边会对utilit有较大损害，所以一般都是添加边）。

作者发现在state-of-art的方法中，加边的策略都没有考虑到图的结构特征，特别是没有考虑到朋友（相邻节点）之间的相似性。因此，他们认为可以通过graph embedding之间的比较，在匿名化的图上检测假边，从而进行恢复。为了证实，用了两种当前效果最好的图匿名化算法——k-DA 和 SalaDP来进行实验。

这篇文章的贡献有：

1. 检测了匿名化图中边的合理性（plausibility）：计算匿名化后的图节点的embedding，对于每一条边，计算两个端点embedding的相似度，以相似度来反映plausibility。相似度越低，代表这条边越不可信。
2. 图恢复： 用plausibility来检测假边， 并用AUC来度量假边检测的准确度（不固定分类的threshold）。在多个真实数据集上的实验表明有很好的效果（AUC=0.95）。然后用混合高斯分布的生成模型来确定分类的阈值，即，假设真实的边与假边遵循两种不同的高斯分布，然后用最大化后验概率的方法来确定分类阈值。
3. privacy damage：对两种匿名化机制，计算原图、匿名化后的图和恢复后的图的privacy loss，以此来说明作者的图恢复攻击对这两种匿名化机制的影响。
4. Enhancing Graph Anonymization: 提出了一种产生假边的方法， 可以让假边更合理、难以被检测出来，因此更难以恢复，同时还保留了更多utility。

总的来说，就是在用k-DA、SalaDP两种匿名化机制作用的图上进行了图恢复攻击，评估了这种攻击对隐私保护的影响，最后提出了更好的图匿名化机制，可以更难被恢复、有更好的utility。

Preliminaries

1. 记号

2. k-DA

假设攻击者知道原图中每一个节点的度数，即一个用户的朋友数量。k-DA遵循数据库k-anonymity的定义，修改原图，使得每一个节点都有至少k-1个节点和它 度数相同。

k-DA算法分成两步： 第一步是用动态规划得到一个符合k-anonymity的节点度数序列。第二步是加边，对每一个节点维护一个还需要添加的边数量，称为 residual degree， 每次给一个节点加边的时候，选择residual degree最高的用户连接。

3. SalaDP

应用差分隐私的定义，其中统计量（被观察的输出）是dK-2 series，它的每一项形如(i, j) k, 表示连接度数为i 和度数为j 的节点的边条数为k。

SalaDP首先对原图的dK-2 series的每一项加入拉普拉斯噪声，然后根据新的dK-2 series加边， 加边是随机的。

上述两种算法主要都是添加假边，但是也有删掉小部分边的情况。

4. threat model

攻击者只知道匿名化后的图 Ga,和使用的匿名化机制A。

攻击者要试图检测出Ga中的假边，恢复图，并最终在恢复后的图上进行用户隐私的推断。

Edge Plausibility

采用graph embedding的方法将节点映射到embedding space，计算节点的相似度，最终量化边的plausibility。

graph embedding大家应该都很熟悉就不讲了，这里用了DeepWalk，计算loss的时候用了negative mining，用SGD来学习参数。

一条边的plausibility 的定义： 两个端点embedding的余弦相似度，即：

$$s_{\mathcal{A}}\left(u, u^{\prime}\right)=\frac{f(u) \cdot f\left(u^{\prime}\right)}{\|f(u)\|_{2}\left\|f\left(u^{\prime}\right)\right\|_{2}}$$

plausibility的取值范围是[-1, 1]。

Graph Recovery

首先用AUC来评价plausibility这个度量能否很好地将假边和真边区分开。然后用混合高斯模型来自动分类。

1. 数据集： 三个real world dataset:
   1. Enron： Enron公司的email communication network
   2. NO： facebook在新奥尔良地区的用户关系
   3. SNAP： McAuley 和 leskovec贡献的数据集
2. 其他相似性度量：

   1. Embeddedness：

      $$\left|\kappa_{\mathcal{A}}(u) \cap \kappa_{\mathcal{A}}\left(u^{\prime}\right)\right|$$

   2. Jaccard Index:

      $$\frac{\left|\kappa_{\mathcal{A}}(u) \cap \kappa_{\mathcal{A}}\left(u^{\prime}\right)\right|}{\left|\kappa_{\mathcal{A}}(u) \cup \kappa_{\mathcal{A}}\left(u^{\prime}\right)\right|}$$

   3. Adamic-Adar score :

      $$\sum_{v \in \kappa_{\mathcal{A}}(u) \cap \kappa_{\mathcal{A}}\left(u^{\prime}\right)} \frac{1}{\log \left|\kappa_{\mathcal{A}}(v)\right|}$$

   4. embedding的欧氏距离：

      $$\left\|f(u)-f\left(u^{\prime}\right)\right\|_{2}$$

   5. embedding的Bray-Curtis距离：

      $$\frac{\sum_{i=1}^{d}\left|f(u)_{i}-f\left(u^{\prime}\right)_{i}\right|}{\sum_{i=1}^{d}\left|f(u)_{i}+f\left(u^{\prime}\right)_{i}\right|}$$

3. 匿名化机制的参数选择：

   对于k-DA，要选择k，分别设置k为50，75，100。 对于SalaDP，要选择差分隐私的ε。 ε越小，对隐私的保护越严格（即改变输入之后的随机化输出函数与改变前的输出差别小于e^ε）.这里分别选择ε=10， 50 和100.

   同时，通过交叉检验选择Random Walk的超参数Walk length、 Walk times和embedding的维数d

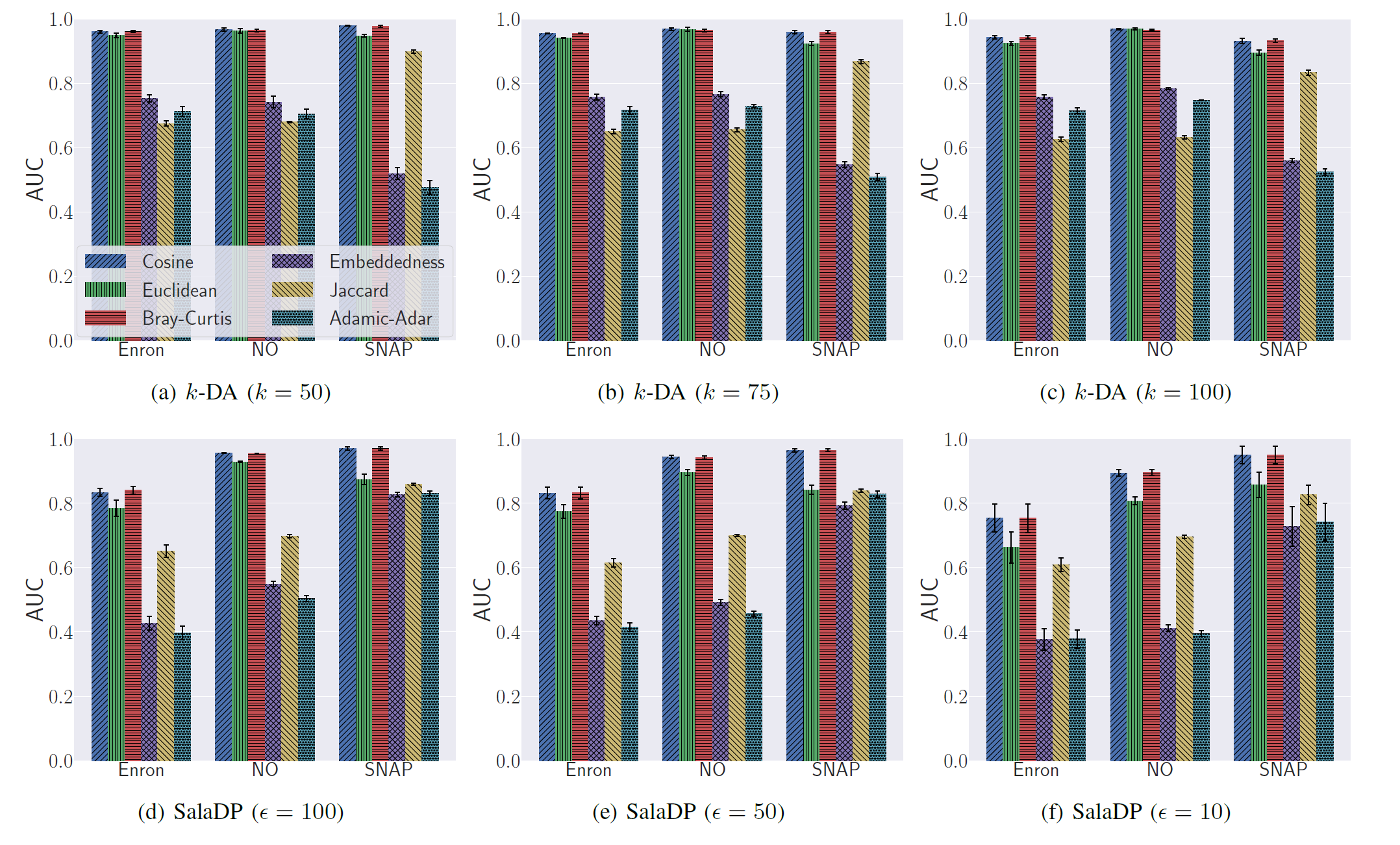
4. plausibility的效果：一般情况下可以取得0.95的AUC，SalaDP在SNAP上的效果最好，AUC=0.971,原因可能是SNAP的平均度数最高，导致dK-2 series最为分散，SNAP在其中添加了数量更多的假边，所以假边检测更容易。但是SalaDP在Enron数据集上效果最差，AUC在0.76到0.83之间。

   fig3中可以看出余弦相似度比另外两个基于embedding的度量如欧式距离和Bray-CurtisAUC略高一点点，而这三个度量比传统的基于邻域的度量效果显著更优。

   

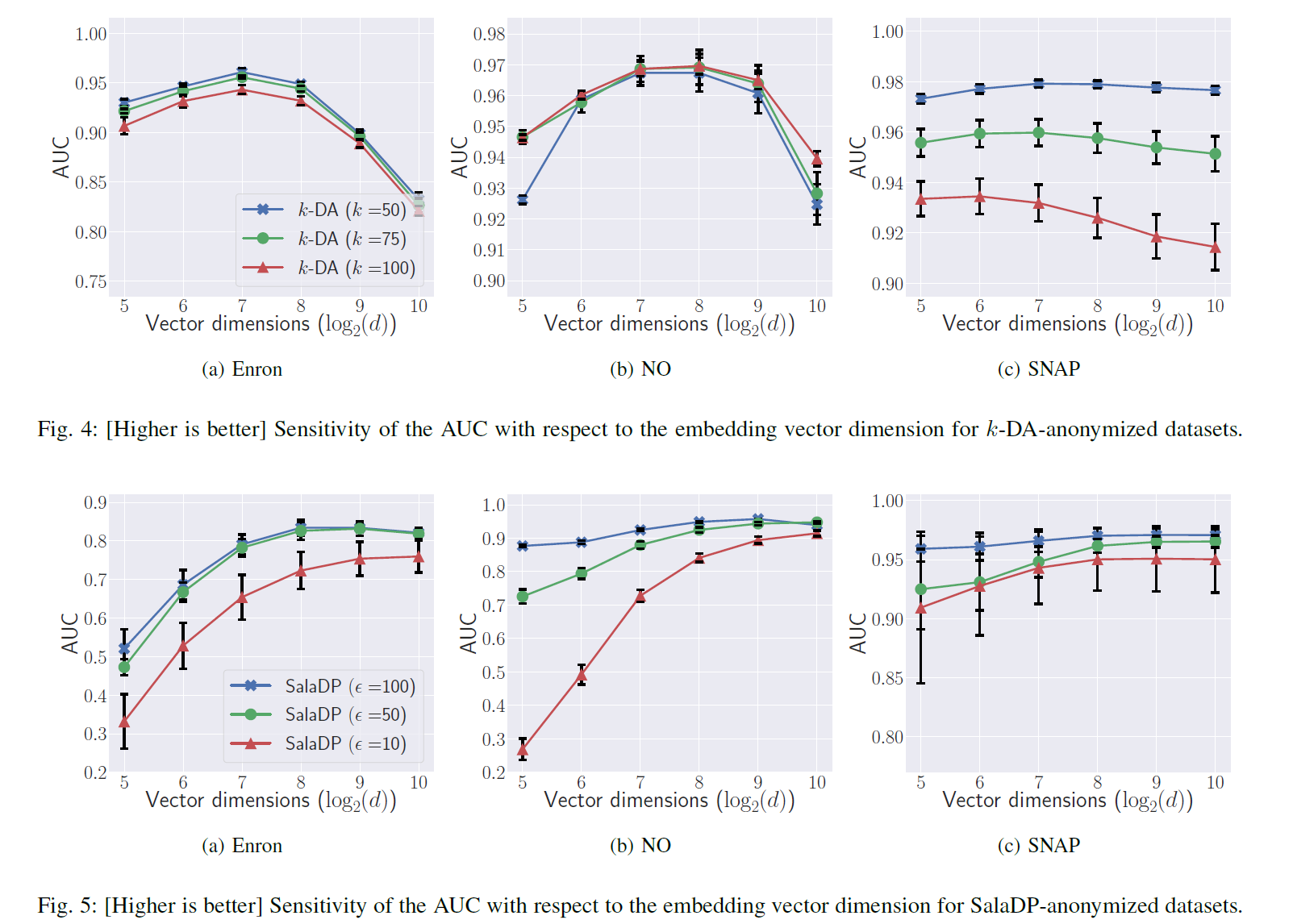
5. random walk超参数的选择： 经过evaluation发现基本上AUC随着walk length 和 walk times增加而增加，不过当两者达到60 的时候增加速度就比较缓慢了。 而对于不同的匿名化机制，embedding 维度d的最优选择不同，对于k-DA是128， 对于Sala DP是512.如图所示。

   

6. 用高斯混合模型和最大似然法分类：如图，可以看到真边和假边的plausibility遵循两种不同的高斯分布：

   

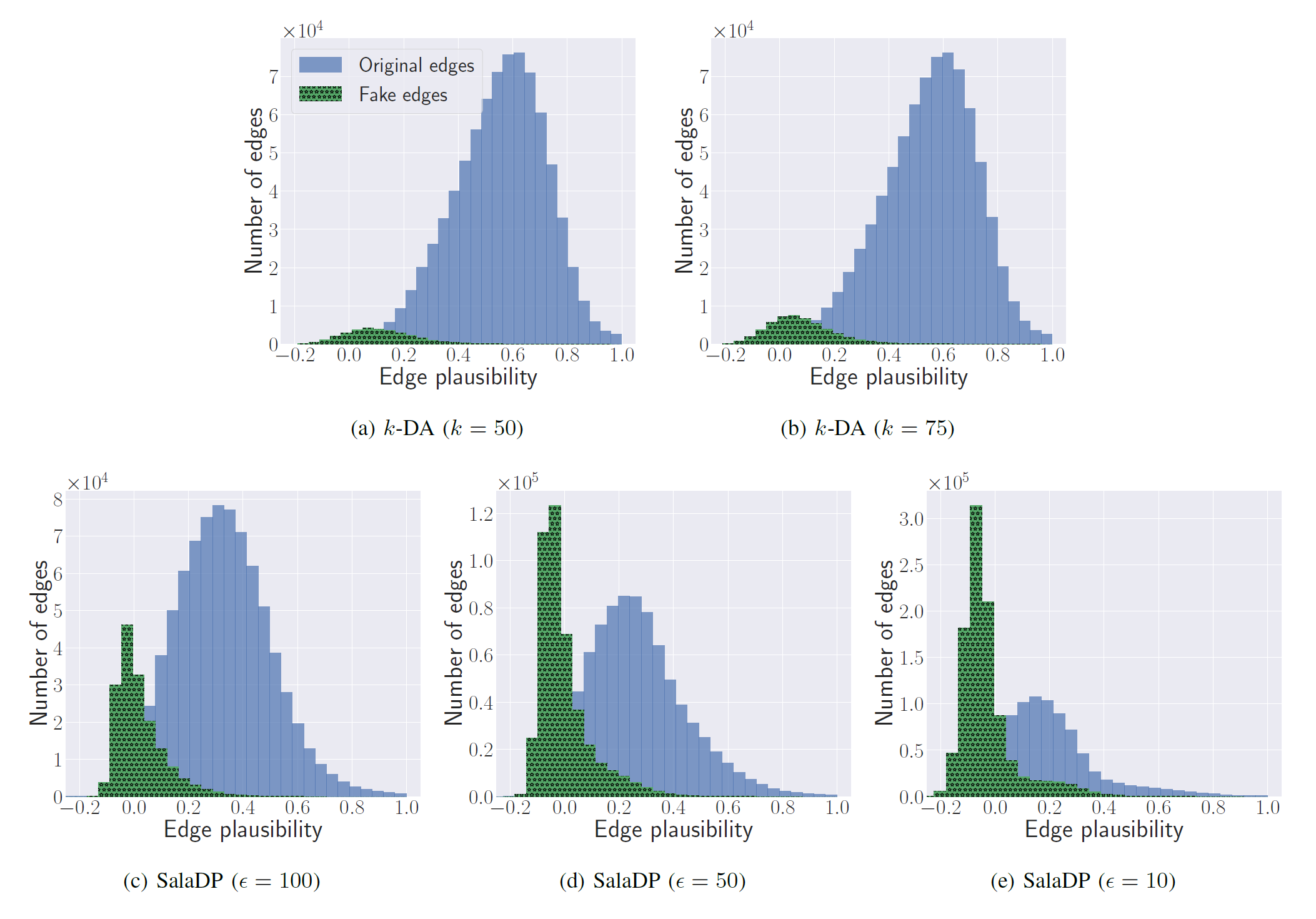
   所以可以用混合高斯模型来拟合所有边的plausibility，这样在给出一条边的plausibility时，可以计算它属于真/假的后验概率，将边分类到后验概率较大的类中去。

   混合高斯模型的具体定义：两个随机变量 S和B， B=0表示真边、B=1表示假边； S表示plausibility。则：

   $$p\left(\mathcal{S}=s_{\mathcal{A}}\left(u, u^{\prime}\right)\right)=\sum_{i \in\{0,1\}} w_{i} N\left(s_{\mathcal{A}}\left(u, u^{\prime}\right) | \mu_{i}, \sigma_{i}\right)$$

   （全概率公式）其中，wi是P(B=0)或P(B=1) .

   模型训练： 使用EM算法（最大期望算法，一种框架），包括两个步骤：

   • E-step：根据数据集，计算每条边属于正/负类的后验概率。

     $$\begin{array}{l} P\left(\mathcal{B}=0 | s_{\mathcal{A}}\left(u, u^{\prime}\right)\right)=\frac{w_{0} N\left(s_{\mathcal{A}}\left(u, u^{\prime}\right) | \mu_{0}, \sigma_{0}\right)}{\sum_{i \in\{0,1\}} w_{i} N\left(s_{\mathcal{A}}\left(u, u^{\prime}\right) | \mu_{i}, \sigma_{i}\right)} \\ P\left(\mathcal{B}=1 | s_{\mathcal{A}}\left(u, u^{\prime}\right)\right)=\frac{w_{1} N\left(s_{\mathcal{A}}\left(u, u^{\prime}\right) | \mu_{1}, \sigma_{1}\right)}{\sum_{i \in\{0,1\}} w_{i} N\left(s_{\mathcal{A}}\left(u, u^{\prime}\right) | \mu_{i}, \sigma_{i}\right)} \end{array}$$

   • M-step： 使用最大似然估计更新参数μ、σ和w

   参数初始化是随机的。

   训练完了之后用这个模型去分类，检测假边，把假边删掉，得到恢复后的图。

7. 结果：

   在大部分情况都取得了比较好的f1-score。且一般隐私保护级别增加，f1-score越高，这可能是因为隐私级别越高就需要加入更多的假边，这种时候正例更多利于学习。

   

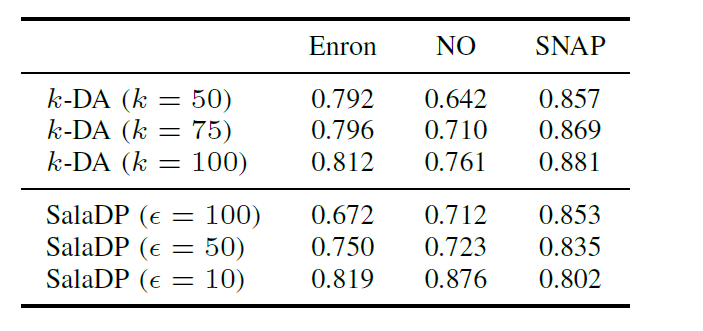
Privacy Loss

两种匿名化机制都提供了对应的隐私保证（k-DA是k-anonymity， SalaDP是ε-差分隐私）。 经过上述的graph recovery之后，隐私保证可能就会不成立了。这里分别对两种匿名化机制设计了privacy loss 度量。

1. k-DA： k-DA是假设攻击者知道用户的度数，并且可以通过这个知识来识别个体。如果Gr比Ga在节点度数上与原图G更相似，则在Gr上更容易展开攻击。所以通过定义GA和G、 Gr和G的度数相似度来衡量privacy loss：

   $$\Delta_{\mathcal{A}}=\frac{\sum_{u \in \mathcal{U}}\left\|\kappa(u)|-| \kappa_{\mathcal{A}}(u)\right\|}{|\mathcal{U}|}$$

   即平均度数差。

2. SalaDP：SalaDP是往kD-2 series中加入拉普拉斯噪声，所以要衡量恢复前和恢复后的噪声之间的差别：

   原图G中kD-2 series中的项定义为：

   $$r_{i, j}(\mathcal{G})=\left|\left\{\left\{u, u^{\prime}\right\}\left|\left\{u, u^{\prime}\right\} \in \mathcal{E} \wedge\right| \kappa(u)|=i \wedge| \kappa\left(u^{\prime}\right) |=j\right\}\right|$$

   恢复后Gr往G中添加的噪声定义为：（Ga对应定义相同）

   $$\zeta_{i, j}\left(\mathcal{G}, \mathcal{G}_{\mathcal{R}}\right)=r_{i, j}\left(\mathcal{G}_{\mathcal{R}}\right)-r_{i, j}(\mathcal{G})$$

   用两种策略来度量privacy loss：

   1. 平均噪声之差：

      Ga的噪声是kD-2 series中所有项的平均噪声。 因为noise是一个随机变量，所以用SalaDP做了100次匿名化，得到100个Li,j （G, Ga) 和100个Li，j (G, Gr)，每一项的噪声就是100次采样的平均。

      $$\bar{\zeta}_{i, j}\left(\mathcal{G}, \mathcal{G}_{\mathcal{A}}\right)=\frac{\sum_{t=1}^{100}\left|\zeta_{i, j}\left(\mathcal{G}, \mathcal{G}_{\mathcal{A}}^{t}\right)\right|}{100}$$ $$\zeta_{\mathcal{A}}=\frac{1}{|D(\mathcal{G})|} \sum_{r_{i, j}(\mathcal{G )} \in D(\mathcal{G})} \bar{\zeta}_{i, j}\left(\mathcal{G}, \mathcal{G}_{\mathcal{A}}\right)$$

   2. 由于噪声导致的不确定性：用熵来度量不确定性。 首先对每一个项，计算100个样本的香农熵(Shannon entropy), 记为 Hi,j (G, GA), 然后整个图的不确定性就是所有项的平均：

      $$\hat{H}_{\mathcal{A}}=\frac{1}{|D(\mathcal{G})|} \sum_{r_{i, j}(\mathcal{G}) \in D(\mathcal{G})} \hat{H}_{i, j}\left(\mathcal{G}, \mathcal{G}_{\mathcal{A}}\right)$$

评估的结果：

1. k-DA： Δr比ΔA小，说明恢复后的图度数更接近原图，说明图恢复确实造成了隐私损失。不过在NO数据集上，两者最接近，这可能是因为NO数据集本身就已经很接近k-匿名性了。

   

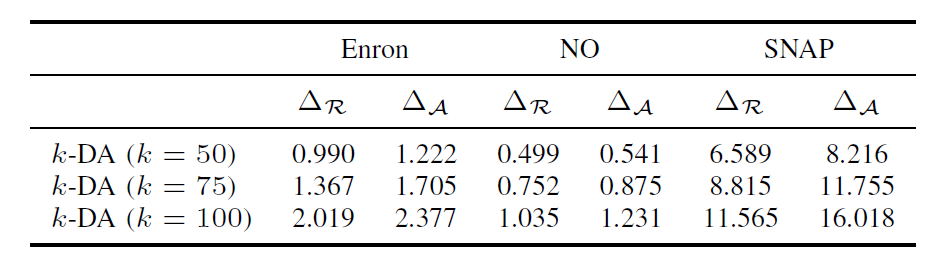
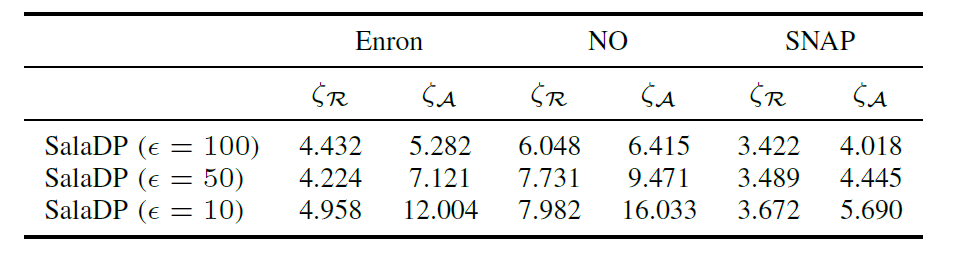
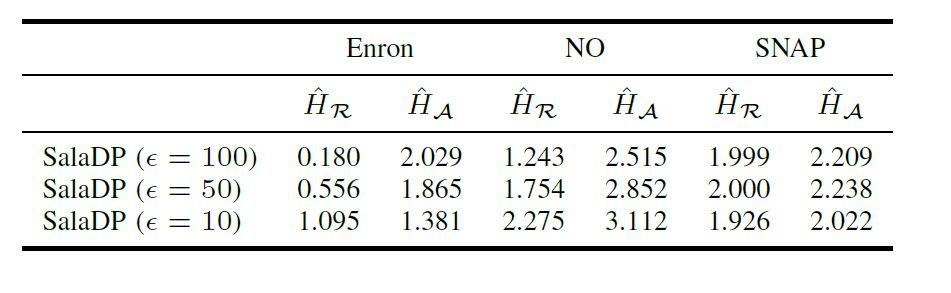
2. SalaDP：ε越小，即隐私保护越严格，需要加入的噪声就越多；但是熵并不一定总是增加的。未来可以研究ε和数据集特征对于entropy相对下降幅度的关系。

   

   

在图上进行de-anonymized攻击： 分别在恢复前、恢复后的图上进行了NS-attack，然而出乎意料的是，在恢复后的图上攻击的效果并没有比恢复前好多少，根据Ji et al的评估，NS-attack有时候在anonymous图上的效果比在原图上还要好（这个评估好像就没什么意思了…

作者认为graph de-anonymize在恢复后的图上效果没有显著变好，是因为这种图去匿名化攻击是基于一个更强的假设（知道一些已经对齐上的seed nodes，并且知道原图的一部分或者具有节点身份信息的子图），所以用图去匿名化的效果来衡量图恢复的效果并不妥当，所以才用privacy loss来度量。

Enhancing Graph Anonymization

方法

要产生更合理可信的边，就要产生和原来边的分布更接近的边。所以首先，拿到原始数据的时候，对原始边计算plausibility，然后学习高斯模型。然后可以把k-DA和SalaDP的算法流程中，对节点u选择要加边的邻居的过程修改为：

1. 产生邻居候选集
2. 计算候选集中，每一条边的plausibility， 对每一个plausibility，用之前学到的高斯模型计算概率密度，将概率密度作为每一个候选节点的权重，最后根据权重从候选集中选出相应的m个节点，与u连边。

要强调，因为算法的第一步没有变，所以修改之后的算法仍然可以达到k-anonymity或者ε-差分隐私的效果。

评估

评估修改后的算法，分为三个方面： 假边检测、图的utility以及去匿名化的效果。用修改后的算法对图进行匿名化，得到图Gf

1. fake edge detection： 仍计算plausibility、AUC。

   所有情况下AUC都有所下降，最多下降了35%。k-DA的AUC下降较多，而SalaDP下降更少，但效果仍然比较显著。并且，真、假边的高斯分布有很大部分是重叠的（不过假边的plausibility仍然较低），说明第4节的混合高斯模型不太能将两者区分开来了，Gf上的f1-score只有0.37，下降了50%。

   

2. graph utility：图数据被公布一般是给第三方做研究或者开发商业应用的，所以图匿名化要平衡隐私保护与可用性。有一些图的属性可以度量可用性，这里用了三个： 度数分布、 eigencentrality和triangle count。 eigencentrality反映的是节点在图中的重要性或影响力，基于邻接矩阵的特征向量，为每一个节点赋一个centrality score；triangle count是所有节点，参与的三角形个数的总和，它反映图的连接性（connectivity)

   通过比较Gf 和G、 Ga和G这三个度量的相似度来比较utility。

   

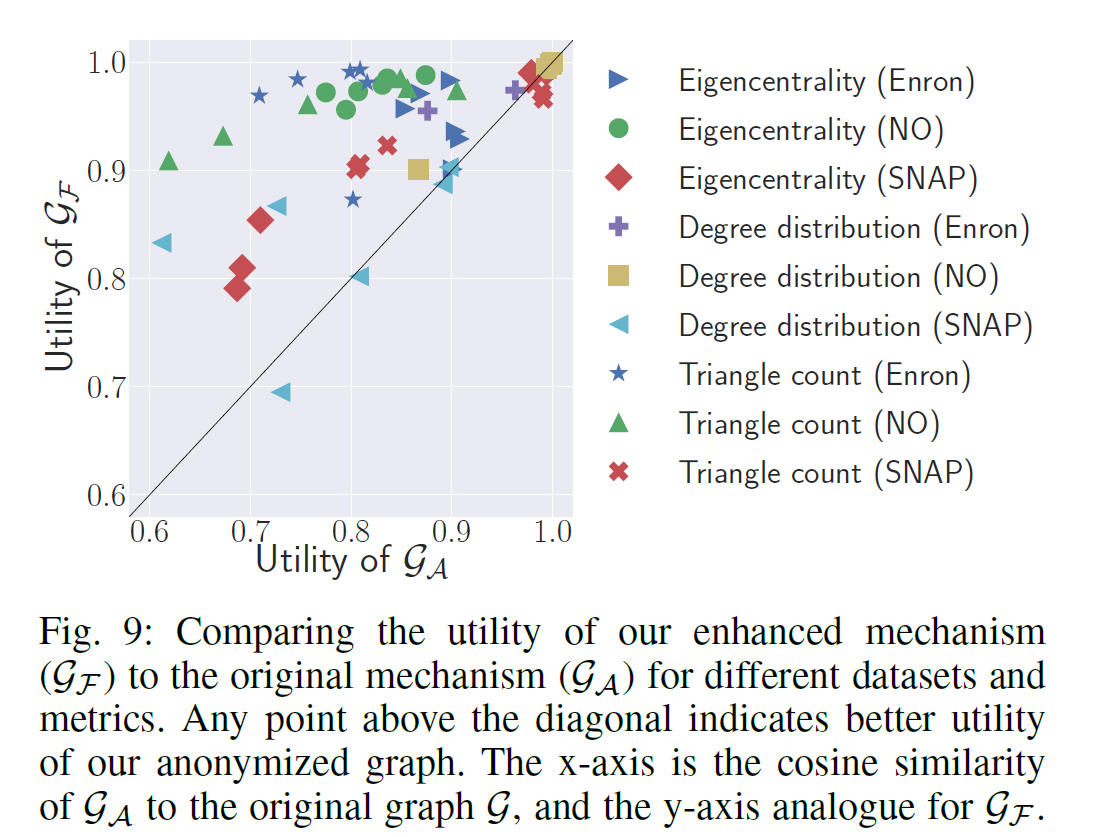
   纵轴是Gf的utility，横轴是Ga，大部分点分布在左上角，说明Gf的utility总体来说更好。

3. de-anonymize： 用NS-attack来去匿名化。 NS-attack假设攻击者有一张包含节点identity的auxiliary graph，还有这张已经匿名化的图(target graph），ta要将auxiliary graph中的节点与target graph中的节点对齐。 并且，其中已经有小部分的节点对齐了，这部分称为seed nodes，攻击者可以通过者小部分对齐上的逐步扩增（propogating）。

   在这个实验中，分别将Ga和Gf作为target graph， 然后从原图G中采样25%的节点，他们的生成子图作为auxiliary graph，其中200个度数最高的节点作为seed nodes。进行NS-attack后计算能成功对齐的节点数量（越少越好）：

   

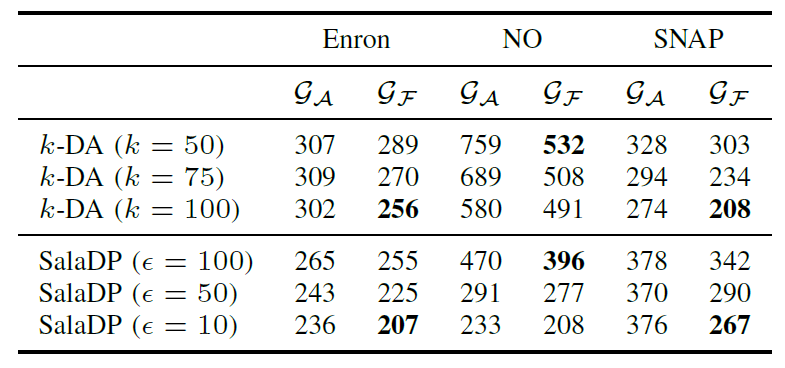
   所有情况下都是在图Gf上更好，即更难去匿名化。

   不仅正确对齐的节点更少，错误对齐的节点也更少了（说明NS-attack的传播（propagate）能力在优化后的图上更弱）

Conclusion

本文指出了当前图匿名化主流算法的缺陷：加边的时候没考虑到相邻节点的结构相似性。提出了一种plausibility度量，可以区分假边和真边，并依此进行图恢复，会减弱本来的匿名化机制的效力。为了弥补这个缺陷，提出了一种基于plausibility的匿名化机制，可以有效抵抗图恢复攻击和去匿名化攻击，并提供更好的utility。

(问题：

1. graph embedding也是在匿名化之后的图上做的，经过干扰之后还会保持原图上的邻居关系吗？graph embedding的相似度还和原图一样吗，如果不一样是不是检测不出来假边了呢？ 个人理解是，匿名化机制因为要保持utility所以干扰的时候应该会选择结构上相近的节点之间链接吧，而且原来就相连的节点仍然是链接的，相似度会有干扰但还是差不多的
2. 匿名化算法有删除边的情况，对于这样的怎么recover呢？ 个人理解是，有一种办法就是假设整个图是全链接的，对没有链接的两两计算plausibility，最高的k个看做是被删除的边连起来，只不过这样复杂度太高了)